自然な形 artifacts natural form
自然な形とは何か。自然の形との違い何か。「自然な」は「自然の」とは全く異なるものとして扱っている。「自然な」何かは人工物である。人の手によって形作られているものを指している。ただ,形を構成する素材の特性に素直になれば素直になるほど,そして,その形が受ける力に真っすぐに寄り添おうとするほど,その形は「自然な」ものとなる。その意味では,「自然の形」で言及した蜘蛛の巣の形を説明する中で定義された懸垂曲線を示すロープもしくは,これを基本的な造形原理とする弦および膜構造もおそらく「自然な形」と称していいだろうと考えている。What is the difference between shapes found in nature and natural forms? I treat "natural" as something quite different from "found in nature". Something "natural" is just an artifact. It refers to something that has been formed by human hands. But the more honest we are with the properties of the materials from which the form is made, and the more straightforward we are with the forces to which the form is subjected, the more 'natural' the form becomes. In this sense, I think that a rope showing the suspension curve defined in the description of the spider's web in the section on "shapes of nature", or a string and membrane structure using this as its basic forming principle, can probably be called a "natural form".
古郷秀一作「たわみ」の形
益子陶芸美術館がある陶芸メッセ・益子の公園の一角に設置された彫刻である古郷秀一氏による「たわみ」を目にしたとき,工学とデザイン・芸術の狭間で楽しくも苦しい模索/もがきを続けている自分にとっては,そこに一つの解答があるような思いを持った。下手な写真で申し訳ないが,後日の差し替えを約束として,このままで許していただきたい。
When I saw the sculpture entitled "Deflection" by Shuichi Furugo installed in a corner of the park at the Ceramics Messe in the town of Mashiko in Tochigi Prefecture, where the Mashiko Ceramic Art Museum is located, I felt as if it spoke to me directly, as a person who has been happily but painfully searching and struggling in the exciting territory that lies between engineering and design and art.
I apologize for the poor quality of this photo, but hope you will forgive me for leaving it as it is, promising to replace it at a later date.
1. 「たわみ」の工学的特徴 1. Engineering Features of "Deflection"
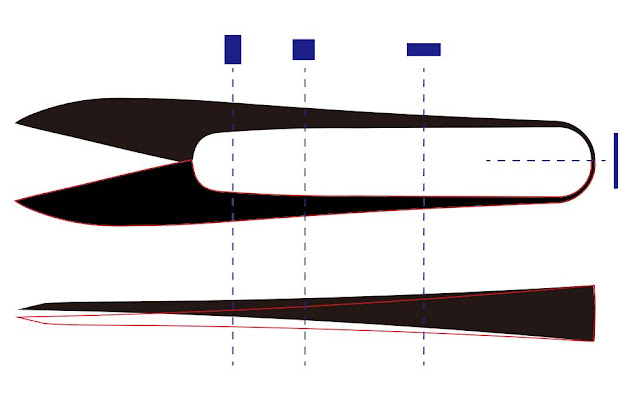
この立体構成の構成要素はシンプルな長方形状の5枚の平板である。板厚以外は長さ,幅,材質すべてが同一であるように見える。この5枚組の平板セットが,2つの異なる最も基本的な境界条件化に置かれている。一つ目の境界条件では,この長方形板セットの重心位置のみが支えられ(幾何学的境界条件),その他の部位は重力による鉛直方向下向きの力(物体力)のみを受ける(力学的境界条件)。
The components of this three-dimensional configuration are five simple rectangular flat plates. They seem to be identical in length, width, and material except for their thickness. This set of five plates is subjected to two different and most basic boundary conditionings in basic Mechanical Engineering.
In the first boundary condition, only the center of gravity of the rectangular plate set is supported (geometric boundary condition), while the other parts of the rectangular plate set are subjected only to vertical downward force/body force due to gravity (mechanical boundary condition).
重心位置での支持点を通る鉛直方向の軸は,この造形の左右対称の対称軸となり,この支持点での平板の断面の向きは水平方向であることがイメージできる。この状況は,慣れないと不思議な感じもするあろうが,この縦横比の高い(ひょろ長い)片持ち板による立体構成の右半分と左半分それぞれが,対称軸上で背中合わせでクランプ(移動も回転もできない状態)されていると見ることができる。
The vertical axis passing through the support point at the center of gravity becomes the axis of symmetry of this sculpture, and the orientation of the cross-section of the flat plate at this support point can be imagined to be horizontal. This situation may seem strange if you are not familiar with it, but you can see that the right half and the left half of this three-dimensional composition of cantilevered plates with a high aspect ratio (i.e. the length to the width) are clamped back-to-back on the axis of symmetry in which the cross-section is neither moving nor rotating.
図1 5枚の鉄板による2種類の立体構成
図2 中心軸を左右対称の対称軸とする片持ち状態(手前)と両端単純支持状態(奥)
2. 「たわみ」の構造解析 Structural analysis of the deflection
2.1. 中央のみの柱で支えられた「たわみ」 "Deflection" supported by a central column only
この形状では,中央の柱の長軸を対象軸とみなすなら,大雑把ではあるが,この造形は左右対称であり,その中央に鉛直方向に伸びる対象軸と交差する鉄板の断面は右にも左にもよらない,いいかえると断面の運動が固定されている状況にあるとみなすことができる。
In this shape, if the long axis of the central pillar is regarded as the symmetry axis, the shape is symmetrical, and the cross-section of the steel plate that intersects the axis rotates neither clockwise nor counterclockwise.
そこで,ここでは,この造形の右半分だけを解析対象とし,中央部分での自由度(水平方向,前後方向,鉛直方向)すべてが空間に拘束されたとした。この5枚の片持ち梁はすべて重力による自重(物体力)を受けているとして解析を行った。
Therefore, only the right half of the model is considered here, and all the degrees of freedom of the central part are assumed to be constrained in space. All five cantilever beams are assumed to be under their own weight due to gravity (body force).
図3 中央のみに柱が設置された「たわみ」の応力分布とシミュレートされた変形(たわみ)Stress distribution and simulated deformations (deflections) for "deflection" supported with a column in the centre
図1の写真と比較してもらうと確認できるのだが,図3でシミュレートされた変形形状(たわみ)と造形物の形状に類似性があることは否定できないと考える。むしろ,恐れながらも,『古郷のたわみは自然である』と主張したいほどである。
There seems to be a similarity between the deformed shape (deflection) simulated in Fig. 3 and the shape of the sculpture. Rather, I would like to assert that the deflection of Furugo is a natural form from a mechanic’s point of view also.
図4 右半分のたわみの比較 Comparison of the deflections in the right half
真横から見るとその傾向はさらに際立って確認できる。この曲線は後章にてより材料力学的に触れることにするが,初等的な梁理論で説明できるたわみ曲線である。実物の中央が上図の左端に位置するのだが,その部分にもっとも強い応力が掛かっていることは実感をもって理解できると思う。その反対に,大きく垂れ下がった右端は,その変形の大きさからついつい勘違いされるのだが,応力はほとんどかかっていない。
The trend is even more pronounced when viewed from the side (Fig.4). This is a deflection curve that can be explained by elementary beam theory. The centre of the actual beams is at the left end of the diagram, and it is easy to see that the stresses are strongest around this area. Conversely, the right end of the beam, which hangs down a lot, is not stressed at all, although it is often misunderstood because of its large deformation.
さらに,ここで気づくべき大きな特徴は,重ねられた5名の板が,上ほど厚みがあり,下に行くほど薄くなっている。その造形の自然さからくる美しさは当然のものとして,『薄ければ薄いほど弱いから,より下に曲がりやすいので当然の造形』とも感じるかもしれないが,実は,厚みがあればあるほど,中央部(左端)には大きな負担がかかっているはずなのだ。厚みがあれば厚いほど曲がりにくくなり,その一方で,それを曲げようとする自重も増えていくわけである。それには,厚くなることで厚みの倍数の3乗分曲がりにくくなる性格と,厚みによって中央部にかかる曲げる力(実はモーメントだが,モーメントも後章で紹介する)は,厚みの倍数のみだけ増加することになり,結局,外見上は短絡的に『薄ければ薄いほど弱いから,より下に曲がりやすいので当然の造形』に見えてしまうが,現実はもっと繊細である。
Furthermore, the main feature to be noticed here is that the five overlapping boards are thicker at the top and thinner at the bottom. The beauty of the naturalness of the shape may be taken for granted, and it may be felt that 'the thinner the plate, the weaker it is, and the more likely it is to bend downwards, so that its deflection is a very natural formation', but in fact, the thicker it is, the greater the burden must be on the central part (left end). The thicker the plate, the more difficult it is to be bent, and on the other hand, the weight of the board, which is the cause of its bending, will also increase in a reciprocal manner.
There is a counterbalance between the fact that the thickness makes it more difficult to bend by a factor of three to the increment ratio to the original thickness, and the fact that the bending force on the center (actually the bending moment, which will also be addressed in a later chapter) increases by a multiple of the thickness.
After all, from the outside, it looks like 'the thinner it is, the weaker it is, and therefore the more likely it is to bend downwards, so it is a natural shape', but in reality it is much subtler.
2.2. 両端が支えられた「たわみ」 A 'deflection' supported at both ends
もう一つの「たわみ」は両サイドに石柱を持つ。よくよく見ると,その端では5枚の厚さの異なる鉄板はお互いに重なり合うことで,やや複雑な力関係にあることがわかるが,ここでは,もう一歩踏み込んだ単純化でモデル化を実施し,構造解析に持っていった。
The other 'deflection' has stone pillars on both sides. On closer inspection, it can be seen that at their ends, the five steel plates of different thicknesses overlap as if closely attached to each other, resulting in a rather complicated force relationship, but here I have taken the model one step further in simplification and brought it to structural analysis.
図5 両端単純支持状態の右半分 The right half of a double-ended simple support
この結果ももう一つの「たわみ」と同じ傾向にあるが,両者の幾何学的境界条件はかなり異なる。
This result also follows the same trend as the previous 'deflection', but the geometrical boundary conditions between the two are quite different.
図6 両端単純支持右半分側面図 Side view of right half of double-ended simple support
この図の左端が両端支持の「たわみ」の中央に位置する。この点を基準に形もたわみ方も左右対称なので,この鉄板の断面は,この点では左右,前後,そして断面の回転は起きない。中央のみが支持されたもう一つの「たわみ」との違いは,この点の鉛直方向の移動に対しては拘束されていない点である。
The left-hand edge of this figure is the centre of the 'deflection' of the structure with supports at both ends. The cross-section of the plate is symmetrical both in shape and deflection with respect to this point, so that no rotation of the cross-section takes place at this central point. The difference from the other "deflection", which is supported only in the centre, is that the vertical movement of this point is not constrained.
さらに,右端そのものには拘束がなく,実物もほぼそうであるが,単に支柱の上に載せられているだけであり,この右端での回転や,わずかではあるが,左右,前後の移動に関しても拘束していない。ただ,支柱としての空間にされた丸太からの反力を受けることで,その形と力のバランスを維持している。
2つの「たわみ」ともに,おおまかにみると,その形は,その造形において使用されている素材に与えられた形と,その形を空間においてどのように固定し,それに対してどのように働きかけるのかによって,ほぼ一意的に決定されるものと言えないことはない。つまり,自然な形の一つなのである。
3. 「たわみ」からたわみの式
「たわみ」を導入として初等的な構造力学でのたわみの定義を紹介する
4. 「たわみ」を計画する
「たわみ」を計画する( の定義)
https://kystrmapsrv.chiba-u.jp/video/V015179/001fXXdwvS7xoXgv02W
「たわみ」を計画する( の定義 )
https://kystrmapsrv.chiba-u.jp/video/V015208/001PhDLFC9l3xYYH1Yt
「たわみ」を計画する(安全の判定と課題説明)
https://kystrmapsrv.chiba-u.jp/video/V015209/001vOPz5cqN0YkJjpfV
アーチの形 The shape of an arch @Engineering of shapes
ここではアーチ橋と呼ばれる形に注目したい。ただ,新潟の信濃川にかかる萬代橋のような石材の積み上げによる橋げたの形は力学的にもアーチであるが,岩国の錦川にかかる錦帯橋の優美な形状もアーチと称されることもあるが,力学的には必ずしも同一のものとは言えないところがある。いずれにしても,その形を構成する材料,構成要素が受け止めることができる力の種類(圧縮or引張orせん断orハイブリッドとしての曲げ)によって,その全体構造である形が大きく支配されているものも「自然な形」の一つであると理解している。
Here I would like to focus on the forms of some constructions which are called arches in a general sense. In the case of bridge girders made of piled up stones, such as those which can be seen in the Bandai Bridge over the Shinano River in Niigata, these shapes, from a mechanical point of view, are arches, while the elegant shapes which can be seen in the Kintai Bridge over the Nishiki River in Iwakuni are also sometimes called arches, but, from a mechanical point of view, they are not necessarily the same. In any case, I have understood that a "natural form" is one whose overall structure, consisting of many components, is largely governed by the materials of the components that make up the form and the type of force (compression, tension, shear, or bending as a hybrid) that the components can take.
 国指定重要文化財「萬代橋(ばんだいばし)」 Bandaibashi Bridge, a National Important Cultural Property
国指定重要文化財「萬代橋(ばんだいばし)」 Bandaibashi Bridge, a National Important Cultural Property
錦帯橋 Kintai Bridge over the Nishiki River in Iwakuni
1. アーチとは What is an arch?
よく耳にするアーチ構造の中で,貝殻や卵の殻を見るような魅力的な曲面を持った建造物の外見を指している場合もある。あながち間違いではないが,むしろ,大局的にみてはそうなのかもしれないが,構造要素的いいかえると力学的に単純化したアーチ要素としては,海外の教会の構造の一部に見られるように,圧縮のみを受け止めることができるであろうと思われる素材,その多くは石材か,によって高く大空間を構成している構造を構成する要素であると理解していたほうが,間違いは少ないように思われる。
Among the arch structures we often hear about, we may include the appearance of a building with an attractive curved surface, like a seashell or eggshell. This understanding of the shape may not be wrong if we are speaking in broad terms, but I think that the name "arch" should be limited to a mechanically simplified arch element, made of a material, often stone, which seems to be able to take only compression, as is the case in some of the structures found in foreign churches and the like.
といっても,アーチのようでアーチでないもののどこが悪いのかとの疑問も出てくるであろう。もちろんそこに善悪があるわけではなく,その形を構成する構造要素が受ける,もしくは受け止めることができる力の種類が全く異なってくることに大事な論点がある。中途半端な外見の類似性だけで早とちりをしてしまうと,大げさに言えば災害にもつながってしまう。確かに,これは言い過ぎかもしれないが,材料の最適配置,スマートストラクチャなどを考え始めると,このあたりの繊細さは必須となってくる。
However, it may be asked what is wrong with an arch that is not an arch. Of course, there is no right or wrong in this, but the important point is that the structural elements that make up this kind of form can receive very different kinds of forces even though the overall appearance is similar to an arch.
To make hasty judgments on the basis of superficial similarities in appearance can lead, to put it bluntly, to disaster. Indeed, this may be an exaggeration, but when we start to think about the optimal arrangement of materials, smart structures, etc., this kind of subtlety becomes essential.
アーチであるものは,その基本の形を成す部分においては,その構造要素に圧縮応力のみが掛かるように設計されなければならない。もし少しでも,そうでない応力,つまり引張応力やせん断応力が掛かってしまうと,石材やレンガや鉄筋が入らないコンクリートのように,もろくも壊れてしまうことは容易に想像できると思う。主構造が石材を中心としたもので,柱と柱との間をつなぐためにはどうしてもアーチ形状にならなければならないわけも,その構造を構成するすべての部位において純粋に圧縮のみが掛からなければ,その構造体は脆弱なものとなる可能性があるからである。
An arch, in its basic form, must be designed so that its structural elements are subjected only to compressive stresses. It is easy to imagine that if any other stresses were to be applied, i.e. tensile or shear stresses, it would break down as fragilely as stone, brick or unreinforced concrete. The reason why a structure which consists mainly of stone must be arched when the arches connect the tops of two pillars that are distant from each other is that the structure may be fragile if it is not subjected purely to compression in all its parts.
図1 旧ロイヤルカナダ銀行(Crew Collective & Cafe in Montreal)の空間を支えるアーチ状の構造
2. アーチのレビュー review of arches
これまでに何気なく見てきてしまった形の中にもアーチなるものはたくさんあった。なんでもそうなのだが,このように教材としてまとめていると,その見方がなんと不注意でボーとしていたか自責の念に駆られる。といっても仕方がないので,手元にある視点のボケた写真でもないよりかは伝えるべきことの参考になるかと思い,ここでレビューしてみたい。
There were many arches in the shapes that I have seen casually so far. As is the case with anything, when I compile the photos again as a teaching material, I am reminded of how careless and lax I have been in looking at them. So I thought that even an unfocused photograph at hand would be better than nothing, and I would like to review some arches I have seen so far, hoping that it will help me to convey what I want to explain to you about arches from a basic structural mechanics point of view.
図2 浅野川大橋,金沢市 Asano River Bridge, Kanazawa
金沢市の浅野川にかかるアーチ橋である。橋げた間をつなぐ大きなアーチ状の形が特徴的であると同時に,海外でも目にすることができる普遍的な曲面がそこにある。橋げたからの立ち上がりの部分,中央付近へとのつながり部分の曲面変化に少し癖があるように思われる。それも大正ロマンな何かと捉えると味の一つかなとも考える。それとも,もしかすると,本当の石橋ではなく,それらしく見せるための"装飾"としてのレンガパネルの不自然さが隠しきれていないのかもしれない。特に左奥の橋桁の立ち上がりのカーブに少しだけ違和感を感じてしまう。
This is an arch bridge over the Asano River in Kanazawa city. The bridge is characterized by a large arch shape connecting the girders, and at the same time, there is a general curved surface which can be seen in other countries as well. The curvatures of the bridge, however, seem to be a little peculiar in the part where the bridge rises from the girders and where it connects to the centre. I wonder if it might be an example of a retro touch. Or, perhaps, the unnaturalness of the brick panels, which are not functional structural elements but a "decoration" to make the bridge look like a real stone bridge, cannot be concealed. In particular, the curve of the girder on the left side of the bridge looks to me a little awkward or unnatural.
図2 名称未確認,長野県上田市 Name unconfirmed, Ueda City, Nagano Prefecture
使われなくなった旧道にかかる小さな橋である。橋の下に廃線のレールのような跡が見えたが正しいことはわからない。ただの小川かもしれない。そこをまたぐアーチ橋である。アーチ状の開口部の縁を,台形状の断面をもつブロックがきちんと配列されている様子が確認できる。Here is a small bridge over a disused old road. Underneath the bridge I could see what looked like the rails of a disused railway, but I don't know for sure. It could be just a stream. It is an arch bridge spanning the channel. It is possible to see the trapezoidal cross-sectional blocks neatly arranged around the edge of the arched opening.

図3 名称未確認,京都
京都の由緒ある施設の遺構であったように記憶している。このアーチ形状を構成する台形状のブロックは,実はもっとも素直に圧縮を受ける構造要素なっていることが分かる。真正面から撮影するか,その三次元形状をしっかりとっておくべきだったが,単なる同心円の輪切りと径方向のバームクーヘン切りではない形がそこにある。まさにカテナリーカーブを上下反転させた形がそこに見え隠れする。
Regarding the structure pictured here, I recall that these are the remains of a historic facility in Kyoto. The trapezoidal blocks that make up this arch shape are actually the most straightforward structural elements to undergo compression in a pure way. I should have photographed it from the front or taken a good picture of its three-dimensional shape, but this is a shape that is not just a ring of concentric circles or a radial slice of a baumkuchen. It is a catenary curve turned upside down.

図4 内房線トンネル,鋸南
この形,魅力的ではあるが,単純にアーチだよとは言えない。その一番の理由は,この形にかかる外力の方向性である。もっともシンプルなアーチでは,その形にかかる外力は重力による自重,物体力である。アーチたるアーチの形は,この形を構成する要素が純粋に圧縮のみを受け,そのもととなる外力は鉛直方向下向きの一方向のみにおける力のつり合いで成立するものなので,このトンネルのように,その形を構成する自重の影響をはるかに超えた,外部からの鉛直方向のみならず,横方向からも受ける強烈な圧力に耐えなければならない形と異なってくる。
This shape (Fig.2) is also attractive, but I can't simply describe it as an arch. The main reason for this is the directionality of the external force on this shape. In the simplest form of an arch, the external force applied to the shape is the weight of the elements that make up the arch due to gravity. In such an arch, the elements should be purely subjected to compression if it is in an ideal physical state. This tunnel has to withstand intense pressure from outside, not only vertically but also laterally, far beyond the influence of its own weight, so it’s difficult to say that it exhibits the shape of a genuine arch.
3. アーチの基本としての懸垂曲線 -圧縮応力のみを受ける形に向けて The suspension curve as the basis of an arch - towards a form subjected only to compressive stress
『圧縮応力のみを受ける』と聞くと,おやっと思わないだろうか,前述の蜘蛛の巣の形では『引張応力のみを受ける形』と紹介した。引張と圧縮,それを受ける材料にとっては180°異なる力であるが,構造体の主軸つまりその形の特徴の基本となる方向に純粋な力の場が存在するという意味において,この「引張のみを受ける形」と「圧縮のみを受ける形」は等価ともいえる。このことは,蜘蛛の巣が,重力環境下において垂れ下がり,引張応力のみを受け止める中で形成される懸垂曲線,カテナリーカーブがいかなる状況においても維持されるとするとき,重力の方向を上下反転させた瞬間,その形の内部に分布する応力はすべからく圧縮に反転することはイメージしやすいかもしれない。聞いた話ではなるが,バルセロナのガウディによるサグラダ・ファミリア協会の棟の形をデザインする際も懸垂曲線を利用したとのことである。重力下において引張のみを受ける形は,そのまま上下反転させると,圧縮のみを受ける形となるわけである。そういわれると,アーチの形がそれらしく見えてくる。When you hear the words "subjected only to compressive stress", you may be a little bit confused because the aforementioned shape of the spider's web was referred to as a 'tensile only' shape. Although tensile and compressive forces are 180°apart in terms of the materials subjected to them, they are equivalent in the sense that there is a pure field of force in the main axis of the structure, i.e. in the direction that is fundamental to the character of the form. This means that, if the suspension curve, the catenary curve, which is formed by a spider's web hanging down under gravity and receiving only tensile stress, is maintained under all circumstances, it is easy to imagine that the moment the direction of gravity is reversed upwards or downwards, all the stresses distributed inside the form will be reversed to compression. I have heard that Gaudi used the suspension curve in designing the shape of the building of the Sagrada Familia in Barcelona. A shape that undergoes only tension under gravity becomes a shape that undergoes only compression when it is inverted.

図5 同じ長さのケーブルが示す多様な懸垂曲線(支点間のみを変えている)
Various suspension curves shown with the same length of cable
(only the fulcrum interval is changed)
4. 懸垂曲線からのアーチ作成とシミュレーション Creation of an arch from a suspension curve and the simulation
図5の懸垂曲線を上下反転させて,下図のアーチの基本形(赤色の領域)を得る(図6)。理論的には,この領域に沿って構造要素(ここでは台形状の要素)に分割することで,圧縮応力を主に受ける形の再現が可能である(図7)。
The suspension curve is inverted to obtain the basic shape of the arch, which is the red area in Fig.1, shown below. Theoretically, by dividing the arch into structural elements which are the trapezoidal elements along the curve, it is possible to reproduce a form that is predominantly subject to compressive stresses(Fig.7).
図6 上下反転した懸垂曲線に沿ったアーチ形状 An arch shape along a vertical inverted suspension curve
図7 モデル化されたアーチと積み重ねシミュレーション The modelled arch and a stack simulation
図7のモデルを用いて,重力環境下での積み重ねシミュレーションを実施した。理論的には反転懸垂曲線に従う限りはすべての部位において圧縮のみが掛かるので,構造要素間を接合することなく単に重ねることで,この形は安定するはずである。このことを検証するために物理シミュレーターの一つであるWorkingModel2を使用してアーチを構成する要素による積み重ねシミュレーションを実施した。
The model shown in Fig. 7 was used to simulate stacking in a gravity environment. Theoretically, the shape should be stable by simply stacking the structural elements without joining them, since only compression is conveyed at all points in which the neighboring elements contact each other as long as the inverted suspension curve is followed. In order to verify this, a stacking simulation with the elements of the arch was carried out using WorkingModel2, a physical simulator.
図中の赤矢印は要素間の接触力を示す。この状態での接触力はおおむねアーチの形の接線方向と一致しているので,このモデルの形の内部で圧縮応力が主に分布し重力とのバランスを取っていることが確認できる。The red arrows in Fig.7 indicate the contact forces between the trapezoidal elements. Since the contact forces in this state are roughly in the same direction as the tangential direction of the arch shape, it can be confirmed that the compressive stresses are mainly distributed inside the shape of the model and are balanced with the gravity of each element. The red arrows in Fig.1 indicate the contact forces between the trapezoidal elements. Since the contact forces in this state are roughly in the same direction as the tangential direction of the arch shape, it can be confirmed that the compressive stresses are mainly distributed inside the shape of the model and are balanced with the gravity of each element.
この接触力を圧縮応力として再表現したものが下図である。基本的には前述の引張応力を受ける懸垂曲線と同質な形であることが確認できる。青色の短い矢印群が圧縮応力を表している。These contact forces are re-expressed as compressive stress in Fig.8. It can be seen that the shape is the same as the upside-down shape of the tensile suspension curve described before. The short blue arrows represent the compressive stresses (Fig.8).
図8 アーチを構成する一要素に働く圧縮応力と自重のつり合い The balance between the compressive stresses acting on the element of the arch and its own weight
最終的には,積み重ねに成功したものの,わずかなバランスの変化で,この形は崩れてしまうことを確認した。実際に存在するアーチが,長い時を経てもその形状を維持できることに驚きを感じるとともに,その繊細で力強い形を作り出した先人の技術と知恵と,そして素材と形と力との微妙なかかわりに対する直観力の凄さに,あらためて感動してしまう。In the end, although I succeeded in stacking the elements in the simulator, I found that the slightest change in balance would easily cause the shape to collapse. I am amazed that real arches can maintain their shapes after such a long time, and I am impressed again by the skill and wisdom of our ancestors in creating such delicate and powerful forms, and by their intuition about the delicate relationship between material, form and force.
図8 崩壊が進むアーチ
最後に,上の未熟なアーチを元にアーチ橋を作ってみた。恐ろしく簡単な動画で紹介したい。



コメント
コメントを投稿