人工の形 Artificial shapes
テンセグリティ工作を通しての引張と圧縮の確認
手のひらサイズで再現できる引張(応)力と圧縮(応)力が完全に分離した構造体は意外と少ない。一般的な構造体(例えば,椅子,テーブル,自転車などなど)の多くは,まだ解説していない曲げやねじりに関連した構造体内部に分布するより複雑な(応)力のひろがりに対応している。実は,導入の花びらの形は,その高度な(応)力の分布をみせる最たる例ではあったのだが,蜘蛛の巣,フジヤマへの考察を通して,目で直接見ることのできない(応)力なるものを少しは身近なものとして体感できただろうか。
Unexpectedly few structures have a complete separation of tensile and compressive forces that can be reproduced in the palm of your hand. Familiar everyday structures (e.g. chairs, tables, bicycles, etc.) correspond to a more complex spread of (stress) forces distributed inside the structures that strongly relate to bending and torsion, which I have not yet described. In fact, the shape of the petals in the introduction is the best example of such a high level of (stress) force distribution, but I hope that through the discussion so far of the spider's web and Fujiyama as simplified examples from a mechanical viewpoint, you have been able to experience a little more closely the (stress) force that you cannot see directly with your eyes.
ここでは,その意外と実例が少ない『手のひらサイズで再現できる引張(応)力と圧縮(応)力が完全に分離した構造体』として,テンセグリティ(tensegrity )の「工作」を通して,「引張」と「圧縮」の存在とそれらが示す力のバランス,そしてそのバランスの結果としての形の体現に挑戦してもらいたいと考えています。
Here, I would like to challenge you to get your minds round the construction of "tension" and "compression", the balance of these forces, and the shape resulting from this balance through the "construction" of tensegrity as a structure in which tension (stress) and compression (stress) forces are completely separated. I would also like you to think of such a structure that could be reproduced in the palm of your hand, the balance of forces that such a structure would contain, and the embodiment of form resulting from that balance.

1. テンセグリティの特徴 Features of Tensegrity
もう少しかっこいいサンプルがあれば良いのだが,ここでは"工作"つまりみずから作ることが最も大事なので,下の竹による(ほぼ)テンセグリティを紹介したい。竹一本の長さは2mであり,その頂点をつなぐロープは麻縄である。4本の孟宗竹で構成され,その内の一本はかろうじて完全に空間に浮いている。もう少し顕著に浮上させたかったのだが,現場設営ゆえの時間のなさを理由に,ここまでの浮上の具合で止まってしまっている。いつかはリベンジしたいものだとも考えているが,この素材の重さもなかなかのものなので還暦過ぎた身にとってはつらい。余計なことではあるが。
I wish I had a better example, but since "crafting by hand" is the most important thing here, I would like to show you a handmade bamboo tensegrity (see below). The length of each bamboo pole is 2m and the poles are connected by hemp ropes in such a way that the edges of the poles do not touch each other, one of which is completely floating in space.
I would like to have made the floating pole more prominent, but due to the lack of time for on-site construction, work stopped at this point. I would like to do it again someday, but the weight of this material is so great that it is hard for me (already over the age of 60) to deal with. (This is unnecessary information, though.)
さて,一方向からの画像ではなかなか読み取れないが,4本の竹はそれぞれに接触していない。これがこの構造がテンセグリティたるゆえんである。テンセグリティにおいては,それぞれの部材が引張(張力:tension)か圧縮(compression)のみをピュアに受け止めていなければならない。
The four bamboo rods are not in contact with each other, even though it may be difficult to perceive this in this image taken only from one point of view. This lack of contact is the reason why this structure is an example of tensegrity. In tensegrity, each member must be purely under tension or compression as the structure is in an ideal state.
そのためにも,圧縮材がお互いに接触してはならない。それは何故であろうか。少しだけ考えてみて...,そうである,接触してしまうと多かれ少なかれその竹には曲げ(bending)がかかってしまう。Bendegrityと呼称する構造体もないわけではないが,ここではとにかく構造体を構成する構造要素つまり部材はシンプルな単一な力を受けなければならない。
In tensegrity, each component part, or member, must be purely under tension or compression, as the structure is in an ideal state. Why is this so? If the members were in contact with each other, the bamboo would be subjected to bending to a greater of lesser extent, in which case the structure should be seen as an example of bendegrity rather than tensegrity, but here at any rate the structural elements or members of the structure must be subjected to a simple, single force.
そして既に気が付いているかもしれないが,この構造がTensegrityであるためには,竹にかかるロープの取り付け方もかなり重要となる。今回はできるだけ巻きつけ幅を広げないように,できるだけロープと竹の端が「点」でつながるように配慮し,その接合点でおきるであろうモーメント(回転/曲げを起こす能力)の低減を図った。ここでもし思い切り竹に回転を加えてしまうような固縛を与えると,竹に曲げが生じてしてしまうのである。この精度の難しさが,「(ほぼ)テンセグリティ」のゆえんである。And as you may have already noticed, for this structure to be a genuine example of tensegrity, the way the rope is attached to the bamboo is also very important. In this case, I have tried to make the ends of the rope and the bamboo as "point" connected as possible, so as not to increase the wrapping width and to reduce the moment (the ability to cause rotation/bending) that would occur at the junction point if the bamboo were to be tied so tightly that it would be rotated slightly. This difficulty of achieving the precision in which no bending moment is introduced is the reason why I call this bamboo tensegrity ‘almost’ or ‘near’ tensegrity.
2. テンセグリティたる要件
その構造がテンセグリティであるためには,
- その構造を構成する部材にかかる(応)力は,引張か圧縮のどちらかである。
- 圧縮(応)力を受ける部材どうしは接触してはならない。
- 引張材は圧縮材に曲げを与えるように結合してはならない。
さらに慣れてくると, - 圧縮材にかかる(応)力がその圧縮材が耐える得る「座屈荷重」を越えてはならない。
- そのためにも,圧縮材はできるだけ短く抑え,引張材との位置関係を効率よく配置し,大きく展開することが望ましい。
なども出てくる。「座屈荷重」についてはぜひとも後述したい。
3. 選定した枝とストローによるテンセグリティの工作
さて,そろそろ工作に入りたいと思う。花びら同様に身の回りにあるものを有効活用が一番であるが,圧縮材となる棒に引張材となるひも・糸を結びつけるのも意外と難しいかもしれない。対面なら(えせ)職人技の伝承も可能なのだが,そうもいかない。とりあえず,下に工作例として,選定したせんだんの枝4本と麻紐で作ってみたものと,学生さんや展示会参加の子供たちとつくってみたストロー4,5本によるもの,それから,ストロー・テンセグリティ工作熟練者によるやや高度な工作例を示す。
このあと各自において作成し,その力関係を体感してもらいたいテンセグリティの規模は,このように手のひらサイズで,圧縮材が4本以上で構成されたものを考えている。繰り返しとはなるが,素材選択は自由であるが,やはり手っ取り早いのは,環境問題を気にしつつも,ストローと輪ゴムによる立体構成が簡単かもしれない。ただ,多くの人がその立体構成中に圧縮材にかかる(応)力が座屈荷重を越えてしまい,構造崩壊を体験することにはなると思うが,その体験は,むしろ重要である。
このような理由もあるので,次のページでは,ストロー・テンセグリティの作り方を動画で紹介したい。



5. 課題「テンセグリティの工作」の説明
最後に課題「テンセグリティの工作」の説明をしておきたい。課題内容と工作条件を列挙しておく。
- 圧縮材は4本以上で,最低1本の圧縮材は接地することなく浮上するように。
- 圧縮材どうしは接触してはならない。
- 手のひらサイズ以上であれば大きさは自由である。
- 引張と圧縮が均衡する形,つまりハリのある形でなければならない。
- 引張材にたるみがあってはならない。
- 提出する画像は3方向それぞれからの3画像とする。作成したテンセグリティの形態的特徴が読み取れるように配慮して欲しい。
- あとは,基本姿勢としては身近にあるもので構わない。鉛筆とタコ糸でも構成できる。もっとも大事なことは,引張と圧縮の分離であり,その力関係つまり力のバランスが取れた瞬間に現れる「形」に見られる緊張感・ハリを感じ取ってもらうことであります。

【参考】テンセグリティ体験工作コーナーにて@千葉市美術館
トラスの形
「自然の形」に見てきた引張(応)力や圧縮(応)力のみで構成された人工の形の代表例としてトラスを考える。トラスはまさに「人工の形」であるが,その構造内部の力関係,力の伝達,力の配分に関しては自然のものと変わらない。ただ,単純化され再構築されているのである。
1. トラスへの導入
トラスへの導入を作成しました。15分を越えてしまうので,トラス(導入)1,トラス(導入)2の二つに分かれています。続けて視聴してもらうといいかなと思います。また,この資料に対する新規の課題はありません。ご心配なく。
トラス(導入)1のノート(参考までに)
トラス(導入)2のノート(参考までに)
2. トラスを解く(節点法/クレモナの図解法)
以下の2つの解説を視聴して,2つ目の解説にて示されている3つの課題にこたえてください。
課題ごとにアップロードしてください。
トラスを解く(節点法)解説1
https://kystrmapsrv.chiba-u.jp/video/V012254/001ubtkB30R1GoNzYFE
トラスを解く(節点法)解説2
参考ノート
トラスを解く(節点法/クレモナの図解法)解説1ノート
トラスを解く(節点法/クレモナの図解法)解説2ノート
3. トラスを解く(切断法)
以下の解説を視聴して課題にこたえてください。
トラスを解く(切断法)解説1前半
トラスを解く(切断法)解説1後半
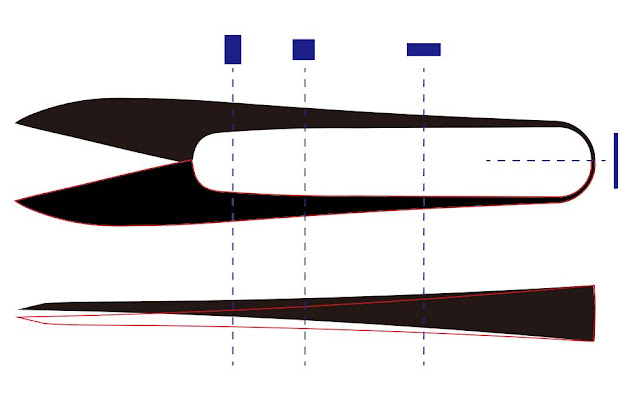
構造力学入門で必ず現れてくる形としてトラスとラーメンがある。トラスを構成する部材(構成要素)は,軸方向の引張か圧縮のみのシンプルな力を伝達するものとして扱われる。それに対して,ラーメンは,複数の部材が剛結合されることで構成されるフレーム構造を指しているので,その部材間に伝達する力は,圧縮,引張の他に,部材の軸を直角に切る力である「せん断力」と,引張と圧縮の合成による「曲げモーメント」を伝達するものと定義される。上の写真は,木製の古い道具であるが,いずれも強烈な曲げを伝達し,形全体で力のバランスを取っているものである。
下に解説PPTと解説を含む動画①と②を置きます。この形については課題設定はしません。②では課題説明も含んでいますが,提出する必要はありません。



コメント
コメントを投稿