自然の形 Shapes of nature
これまでに多くの研究者,創造者が言及してきていることであるが,自然の形にはまちがいなく強烈までの普遍性がある。その形であることに「意味」がある。その「意味」が時には合理性という言葉で表現できることも多い。一見複雑に見え,どことなく恣意的な形であっても,そこにその形であることの必然性があることは誰も否定できないであろう。そして,その必然性が,その形の鑑賞者である人間に,素直な感動を引き起こし,そこに美なるものを感じさせると言ってもそれほど間違ってもいないであろう。そして,それらの形を力のつりあい,変形の学問である構造力学的視点で見るとき,多くの形が期待以上の形の「意味」を示してくる。その「意味」とは,その形であることの必然性・合理性であり,広義の意味での機能そのものをそれらの形は示していることが分かる。
It has been mentioned by many researchers and creators so far that shapes found in nature are undeniably universal. There is "a meaning" to each shape, and the "meaning" is often expressed in terms of rationality. No one can deny that even if a natural shape looks complicated at first glance and has a somewhat arbitrary form, there is an inevitability that the shape has. And it is not so wrong to say that its inevitability causes a human being who is a viewer of the form to be honestly impressed and feel there is something beautiful in it.
If we look at those shapes from the viewpoint of structural mechanics, which is the study of deformation and the balance of forces, many shapes show many more "expected" meanings than we have anticipated. It can be understood that the "meaning" is the inevitability or rationality of being in a particular form and that natural forms in general show the function itself in a broad sense.
この章では,「自然の形」の一例として,花びらの「形」と,その「機能」について考える。花びらは,限られた期間において,雨風,季節によっては降雪に耐えながら,また季節の変わり目の気温の変動にも耐えながらも,効率よくその生の象徴である花を広く展開し,その形を維持しなけれならない。そして,自然の摂理に従い,無駄のない材料配置でその形を展開し,その形を維持し,その形と色により虫に対する視目性を上げなければならない。
ここでは,人為的な意識が介入しにくい領域での普遍的とも言える自然の造形に注目していきたい。
In this chapter, we consider the “shapes” of petals and their “functions” as examples of “natural shapes”. Petals must be able to efficiently compose and maintain a flower that is the symbol of their life while resisting rain, wind and snowfall depending on the season, and temperature fluctuations at the change of seasons, for a limited period. Then, according to the laws of nature, it is necessary for them to develop their shape with a material arrangement that is not wasteful, maintain their shape, and enhance their visibility to insects by means of their shape and color.
Here, I would like to pay attention to the way nature models shapes, which can be said to be universal in areas where artificial intelligence could not easily step in.
花びらの形 Shapes of petal
たまたま目の前に落ちていた花びらである。なんとも不思議な形をしている。その曲面の構成は大胆とも言える。触るとわかるのだが,それはとても柔らかく華奢な素材で構成されている形である。
この形が,右側の丸まった一点のみでその花の中央付近に固定されているだけで,あとの部分は空中に浮いていることが,不思議でならない。なぜ,そのようなきわどい構造で,そう簡単に崩れることのなくその形を維持しているのか,なかなか受け入れがたいものがある。
This is a petal that just happened to fall in front of me. It has a very strange shape. The composition of its curved surface can be said to be bold. When you touch it, you can see that it is composed of very soft and delicate materials.
I think no one can help wondering why this form is fixed to the center of the flower by a single rounded point on the right side, while the rest of the flower floats in the air. It is very difficult to understand why it’s able to keep its shape with such a thin and organic structure.
1. 花びらの形 Shapes of petal
まずは足元の草花から見てみよう。どのような種類の草や花が目に入っただろうか。小さいものか,大きいものか,その茎の形は円柱状なのか,角柱っぽいものなのか。その葉は薄いのか,肉厚なのか。それは,ひょろ長いのか,幅広いのか。その葉は曲面状なのか平面状なのか。そして,はかないほど軟い素材で構成される傾向にある花びらは,葉同様に多様であり,それぞれの形にそれぞれの意味がある。
Let's start by looking at the grass and flowers underfoot. What kind of grasses and flowers did you see? Are the stems cylindrical or prickly? Are their leaves thin or thick? Are they long or broad? And are the leaves curved or flat? And the petals, which tend to be made of ephemerally soft material, are as diverse as the leaves, and each shape has its own meaning.
そのライフスパンにおいて,重力に耐え,雨風に耐え,時には降雪に耐えなければならない。それらの外乱によって簡単にへし折られてはいけないのである。ひたすら耐えながら成長し光合成を実施しなければならない。または,広く展開し,虫たちの眼にとまらなければならない。つまり構造を保ちつつ,効率の良い太陽光線の取得や誘目性向上を,その形状形成の目的としなければならない。
In the span of its life, it has to withstand gravity, wind and rain, and sometimes snowfall. It must not be easily broken by these disturbances in nature. It has to grow and carry out photosynthesis with its neighboring leaves, while it must also spread out and catch the eye of insects. In other words, the purpose of its shape formation should be to acquire sunlight efficiently and to improve its attractiveness to insects, while maintaining its structure.
2. 花びらの形 ー 曲面を利用した薄くて軟い素材によって構成された形状
2. Petal Shape - A shape composed of thin and soft materials with curved surfaces
前述の視点で今一度,草花を見直してみよう 。下図は柴モクレンの花びらである。言うまでもないが非常に華奢で脆い。短い期間ではあるが,その美しい形状は間違いなく数日間は維持され,我々の目と気持ちを癒してくれる。散り始めた柴モクレンを拾い,静かに触ってみるとその柔らかさその脆さに愕然とするであろう。ここまで軟らかく張りのない素材が,どうしてこのような曲面を維持することができるのか,とても不思議な感じがする。
Let us review the plants again from the viewpoint mentioned above. The petals of Magnolia grandiflora shown below, needless to say, are very slender and fragile. I think, however, we have no doubt that their beautiful shape can be maintained for a few days to soothe our eyes and our minds. If you pick up a magnolia blossom that has begun to fall apart and touch it gently, you will be amazed at how soft and fragile it is. It's highly mysterious how such a soft and limp material can maintain such a sophisticated curved surface.
下の図は,実際の花びら(図1)と,それを3 D スキャン技術により三次元形状測定したものをベースにシェル化し,有限要素法を用いて構造解析をしたものである(図2)。カラーのグラデーションは,直感的に言えば,赤いほど強い力(応力)がかかり,青いほど力がかかっていない状況を示す。相対的に見なければわかりにくい面もあるが,この花びらの付け根付近の赤い部分から花先に向けて青白く分布した応力が,花弁の先まで伝達している様子がうかがえる。つまり,応力を比較的全体で受け止めようとする傾向にあることがわかる。
The figure below (Fig. 2) shows the result of structurally analysing a model of an actual petal (Fig. 1), in which the petal has been transformed into a numerical shell-model based on 3D shape measurements by 3D scanning technology in order to implement structural analysis using the finite element method (Fig. 2). On an intuitive basis, the color gradation indicates that the force (stress) is stronger when it is red and less when it is blue. It is difficult to understand unless you look at it relatively, but we can see that the stress is distributed continuously from the red area near the base of the petal to the tip of the petal with the light-blue gradation. This indicates that the stress tends to distribute evenly across the whole petal, comparatively.
仮に,コピー用紙で花びらもどきを作ってみよう。その花びらの付け根あたりのみをつまんで水平に持ち上げようとしたとき,不用意なままの切り抜きでは,ふにゃりと曲がりとても本物のようなその見た目とは異なる毅然とした姿勢を保つことはできないであろうことは,それほど想像に難しくないであろう。
Now, let's try to make a pseudo-petal with copy paper. I think that it is not so difficult to imagine that it would not be able to keep its resolute posture like the real petal if we tried to lift it up horizontally by pinching only the base of the petal, if we cut out the petal from the paper carelessly.
たぶん,そのふがいない紙片をどうにか自立させようと試行錯誤をしているうちに,人によっては不思議な曲面にたどり着くこともあるかもしれない。その時の形がどことなくこの花びらの形と似ていたら,その形の成り立ちの片鱗に触れたことになる。参考とするためにこの花弁曲面の断面分布を図3に示す。
Perhaps, while trying to make a feeble piece of paper stand up on its own by trial and error, some of us might end up with a curious-looking curved surface. If the shape of the piece of paper were vaguely similar to the shape of the petal, then we could have a glimpse of how the shape had been formed. The cross-sectional distribution of this petal curve is shown in Fig. 3.
普通に考えるとこのような花弁の形も片持ち梁と同じである。片持ち梁とはその片方が固定され,片方が自由な状態であるが,明らかに固定されてるほうに強い力がかかる。実際は,力というよりは,物を曲げるモーメントによると考えた方が正しい表現であるが,ここでは付け根ほど強い力がかかる,それに従って彼等の内部に強い応力がかかる,というふうに理解しておいても間違いはないであろう。
In general, the shape of the petal is the same as that of a cantilevered beam. As in a cantilevered beam, one side of the petal is fixed and the other side is free, but obviously, the fixed side is subjected to a stronger force. In fact, it is more correct to think of it as a result of the moment of bending rather than a force, but it is correct to understand that, the stronger the force is applied to the root of the cantilever, the stronger the stress occurs inside the root.
ここまでの考察では,おそらくあまり耳にしたことが,むしろ耳にはしたくないだろう力学力学した言葉がたくさん出てきている。ただ,この形の極意を感じ取るためには,これらに対する理解を避けることはできないので,この後それぞれについて簡単に説明するようにしたい。
図1 柴モクレンの花びら
図2 花びらの応力解析(ミーゼス応力)
図3 花びらの断面分布(淡い青色は裏側,裏側の最初のラインが花の中心に固定されている)
3. 花びらの形の意味を読むために必要な技術と知識
ここでは,柴モクレンの花びらに注目する。もう少し時期が早ければキャンパスで舞い散るソメイヨシノの花びらの形に対する実際の分析と考察を紹介ができたのだが,今回は季節的に柴モクレンを題材にする。あと一か月ほど経つと工学部の長屋沿いに林立するタイサンボクの花びらが際物として面白いのだが…
柴モクレンの花びらは,桜の花びら以上に複雑な曲面で構成されている。まさにシェル(貝殻や卵の殻をイメージしてもいいかもしれない)である。それもかなり複雑なシェルである。この軟そうな形は,重力の下、片持ち状態でその形状を保っているわけだが、自重によって、その形の中に分布する内なる力つまり応力のかかり具合は、形のなか全体でできるだけ均等に分散する傾向にあり、固い(工学的な)言い方をすると、全応力設計的な一つの最適形状がそこにある可能性がある。
Skills and knowledge needed to read the meaning of petal shapes
In this article, I'll focus on the petals of the Magnolia grandiflora. If it were a little earlier in the year , I could show you an actual analysis and thoughts on the shape of the petals of the Someiyoshino cherry tree that frolics around the campus. And, in another month or so, another kind petal of the magnolia tree, which is growing along the row of buildings in the Faculty of Engineering, will be a striking sight...
The petals of the magnolia are composed of more complex surfaces than those of cherry blossoms. Each one is exactly like a shell, or, if you will, an eggshell. And it's like a very complicated shell at that. While it seems very strange that this soft and complicated shape would appear to be unable to maintain its cantilevered form under the force of gravity, due to its own weight, yet the internal force or stress distributed within the shape tends to be distributed as evenly as possible throughout the shape, and we find, in hard engineering terms, nothing less than an optimal shape for total stress design.- 3Dスキャン 3D scanning of real things
花びらに限らず,その形の成り立ちを読み解こうとするとき,実物に対する観察を超えるものはないのであるが,実物はその色,テクスチャ,質感などによって,その形は覆われているために,情報過多となり,なかなか素直に形そのものを見抜くことはできない。それ以上に,実物が持つ存在感の強さゆえか,観察者としての未熟さゆえか,実物と対峙するとき,その観察において必須の冷静さをどうしても欠いてしまう傾向にある。そこで,近年,その進化の速度を早めてきている物体の三次元形状を測定する3Dスキャンという技術に頼ることとなる。今となっては,スマホでも3D形状を取得できるのだが,この桜の花びらの3D形状測定には,骨董品と言われつつもレーザー光の反射を利用した高精度な三次元デジタイザ(KONICA MINOLTA 製VIVID910)を使用した。
Although there is no better way to decipher the origin of a form than direct observation of the actual object, such as a petal, it is difficult to perceive the characteristics of the form itself because the actual object is rich in color, texture, etc. on its surface. In short, there is an overload of information.
Furthermore, perhaps because of the strong presence of the real object, or perhaps because of my immaturity as an observer, I have a tendency to lack the calmness that is essential for observation when confronting a real object. For this reason, I've relied on the technology of 3D scanning to measure the 3D shape of objects, which has been evolving at an accelerated pace in recent years. I've used a high-precision 3D digitizer (KONICA MINOLTA VIVID910), which is said to be an antique by my students, to measure the 3D shape of petals, even though it is nowadays possible to obtain 3D shapes even with a smartphone.
図4 三次元デジタイザ(KONICA MINOLTA 製VIVID910)- 3Dスキャンデータのシェル化
3. Shelling of 3D scan data
3Dスキャンされた3D形状は点一つひとつが三次元の座標値を持った点群でその形状が構成される。使用するアプリケーションによるが,この点群における隣接する3点を頂点とする三角形を定義し,この三角形を連続して点群全体に広げることで花びら全体を三角目の網の目つまりメッシュに置き換える。この三角形も多角形の一つであり,このメッシュをポリゴンメッシュと称する(図5)。なかなか正確な表現は難しいが,このポリゴンメッシュは,実物とCADモデルの中間にあるともいえる。CADモデルの中で数理的な処理が可能となるのは,その3Dモデルの形を代数曲線のように数理的な形状関数で置き換える必要がある。ポリゴンメッシュのままでは,実物の形に三角目のネットをかぶせただけのようなものなので,その形状には数理性が担保されていない。CAEの処理にかけられない。
The 3D shape scanned by the measuring equipment is composed of a point cloud in which each point has a three-dimensional coordinate value. Depending on the application, we define a triangle at the top of three adjacent points in the point cloud, and then extend this triangle to the whole point cloud in succession to replace the whole petal with a mesh of small triangles. As a triangle is a kind of polygon, we call the mesh a polygon mesh (Fig. 5). Although it is difficult to express precisely, we may say that this polygon mesh lies somewhere between the real thing and a CAD model. To make possible some mathematical processing in a CAD model, it is necessary to replace the shape of the 3D model with a mathematical shape function such as an algebraic curve. As it is, the polygon mesh is just a net of triangles laid over the shape of the real object, so there seems to be no mathematical assurance of its shape and we cannot analyze the shape with the mathematical treatment that is possible in a CAD-system.
図2,7,8 に示すような応力解析を可能にするには,実物を数理モデルとして再定義しなければならない。花びらのような薄物は,卵の殻や貝殻のような形状であり数理的な定義の上での形であるシェル要素で構成されたものとして再定義されなければならない。 - 図5および図6は,Autodesk社のFusion360によって表示されるポリゴンメッシュと,そのメッシュをFusion360上で,曲線や曲面を生成するためにコンピュータグラフィックスで一般的に採用される数学的モデルであるT-スプライン面で置き換えたCADモデルである。
図5 Autodesk社のFusion360によって表示されるた柴モクレンのポリゴンメッシュ
図6 Fusion360によってCADモデル化された柴モクレンの花びらシェル - 自重を受ける片持ち状態の花びらの有限要素法による応力解析
Stress Analysis of Cantilevered Petals under Own Weight by Finite Element Method
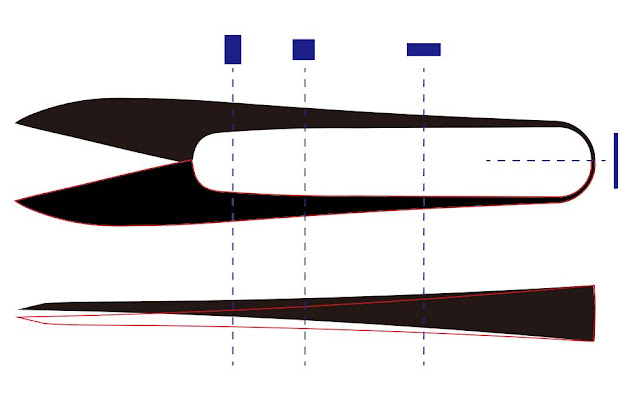
ここまで来てようやく,この形の見えざる極意を可視化するところまでたどり着いた。3DCADモデルとして再定義された花びらシェル(図6)は,有限要素法(任意の形の全体を,4面体や6面体などの単純で小さな形である要素に分解し,要素内での形と力の関係を数理的に定義したのちに全体形に戻し,その形の力学的挙動をシミュレートする手法)に従って,特定の材料物性が与えられ,実際の花びらの取り付けられ方や重力からの影響を,それぞれ,幾何学的境界条件と,力学的境界条件とした環境の下で,応力解析が実施される。この結果が図2そのものである。この花びらを思い切り単純化すると,花びらが伸びている縦軸(長軸)方向と,それに直交する横軸方向それぞれに曲げられた長方形状の曲げ板の短辺の一辺のみを拘束し,残りの辺は自由に,水平に重力環境下にさらしている状況であるとイメージしても良い。下図は,実際の形を再現した花びらモデル(シェルモデル)に対する応力結果(図7)と,そのモデルを平面に投影したモデル(プレートモデル)(図8)との比較を示したものである。この比較より,曲面があることで片持ちされた花びらの付け根にかかる応力が,花びら本来の曲面により,平面ではくびれた部分に集中する傾向にある応力が,比較的形全体に分散し薄められている様子が確認できる。The petal shell is redefined as a 3D CAD model (Fig. 6) according to the finite element method (decomposing the entirety of an arbitrary shape into elements that are simple, small shapes, such as tetrahedrons and hexahedrons, and mathematically defining the relationship between shapes and forces within the elements). In this method, the model is given specific material properties, and stress analysis is carried out under geometric and mechanical boundary conditions respectively for the way the petals are actually attached and the effects of gravity. The figure below shows a comparison of the stress results for a petal model (shell model) that reproduces the actual shape (Fig. 7) and a model that projects the model onto a plane (plate model) (Fig. 8). This comparison shows that the stress at the base of the cantilevered petal is diluted by the curvature of the real petal and is distributed evenly over the entire petal shape except at the root where a greater amount of material tends to be allocated than in other parts of the petal, while the stress tends to be concentrated on the narrower part of the petal in the plane.
そしてさらに重要な点は,その分散された応力が,3D空間に展開していることであり,応力がこのように展開しているということは,同時に花びら上の変形が一方向ではなく複数の方向に入り組んでいることを意味している。これは,平面のコピー用紙の一端を持ち上げても垂れてしまうのに,Uの字に曲げたり,山谷に織ったり,さらには過激にしわを寄せることで,ある程度の曲げに対する剛性が生まれ,片持ちで持ち上げられることと等価なのである。実物では,図7に示された赤色の部分では,他の部位より厚みがあり,体感的にも剛性が高く強度があるように感じ取られる。つまり,花びらはその曲面と材料配置(配置された材料の多さ)によって,効果的な応力分散を実現し,局所的な構造破綻を起こさない工夫がなされ,結果としていわゆる最適設計された構造形態となっていることがわかる。
And more importantly, the distributed stresses are deployed in 3D space, and the fact that the stresses are deployed in this way means that at the same time the deformation on the petals is intricate in multiple directions, not just one. This seems to be equivalent to the fact that paper which is bent into a U-shape, woven and excessively wrinkled, can be lifted up while cantilevered although a flat piece of copy paper may hang down when lifted up. Actually, the area around the root of the natural shape corresponding to the red area shown in Fig. 7 tends to be thicker than the other areas, which gives the petal a function that is stiff and strong. In other words, the curved surface and the material arrangement of the petal (i.e., the amount of material at each place in the petal) enable effective stress dispersion and prevent localized structural failure, resulting in an optimally designed structural form. 図8 花びらモデルを平面に投影したプレート状モデルに対する応力結果
- 応力とは
応力を説明することは意外と困難である。英語ではStressなのだが,日本語では機械系と建築・土木系でその使い方が微妙に異なる。前者で「応力」と言っているものは,後者では「応力度」である。その習慣を今さら崩すのは難しそうである。それだけ「応力」はやっかいなのである。もちろん,初等的な理解で十分なのだが,力そのものが目で見ることができないこともあり,イメージ力が求められる。『力,見えるじゃないか』という人は,おそらく能力者か,それともその「力」によって生じる変形を見て,力を見たような気になっているものと思われる。ところで実は私は見える。その真偽は置いといて,ここでは,まずはこれまで触れてきた花びらに生じている応力なるものが何なのかをイメージしなければならない。
・ヒモにかかる応力
おそらくもっともシンプルな形は,竹のように鉛直方向上向きにすくっと立ち上がりながら圧縮にも曲げにも耐えているような形と全く異なり,自立もできなければ,壁から突き出すこともできない「ヒモ」である。ヒモの響きに慣れない人は,当然ロープでも構わない。もっとシンプルなロープとしては,金太郎飴がごとく,その長軸方向のどこでも全く同じ断面を持ち,その断面積に比べて十二分に長いものをロープもしくはヒモと理解していれば,ミシンに絡まっている縫い糸を見ても,巨大タンカーをつなぎとめているロープを見ても,これはヒモだな,ということになる。
構造要素としてのヒモは,結局,引張力にしか耐えられない構造体を構成する要素である。身の回りにあるヒモを一本準備してほしい。といっても現実のヒモは,ややゴワゴワ(曲げに対しても剛性をもつ,曲がりにくさをもつ)感があるので,これからの理解にとってはややノイズとなるやもしれないので,もう一端には何か錘(大事なマグカップでも良いかもしれない)をぶら下げてもらうと良いかもしれない。そして,それを静かに垂らしてあげると,そこに一つの形が構成される。
ここで考えてみよう。なぜマグカップはそこに宙吊りにされているのだろうか。片方に握りしめている手のひらには確かにカップとわずかなヒモの重さを感じるだろう。その重さの大方はカップが重力によって地球に引き寄せられていることによる「力」の「反力」であることは,すでに知っている。この鉛直方向下向きに垂れ下がったヒモと宙吊りにされたカップで構成される形は,まずはこの「力」と「反力」の釣り合いによるものであることに異論はないであろう。
さて,このときヒモは何をしているのか?これが一番面倒である。実はヒモは気づかれない程度に伸びているのである。「力」による変形が起きている。ただこの表現は必ずしも正しいとも言い切れない。逆に,変形が起こされたものは元の状態に戻りたいから「力」を生み出しているとも言えるのである。高校物理まででは,この変形と力の関係は,「ばねばかりのフックの法則」程度に終始しているので,無理もないことであるが,何歳になってもややこしいものである。
このヒモがカップの重さで少し伸びたとする。その時,ヒモのどの部位が伸びたのだろうか。このヒモがすべてにおいて均一な材料と断面で形成されているなら,どこだろう。手でつかんでいるところだと主張する人もいるかもしれない。もし,ヒモの重さがカップの重さに比べて無視できないほどの存在感があるときにはその回答を否定できない。なぜなら,上に行くほど,その部位のヒモは自分より下のカップの重さと,そこまでの自分自身の重さを支えなければならないからである。しかしここでは,ヒモの重さは無視できる。そうすると,ヒモにもともと局所的な欠陥がないとすると,ある特定の部位で切れてしまうことはミステリーである。
すべての部位は同じに伸びる。「ヒモが少し伸びた」という感覚は,この局所的な均一な微小な伸び(微小変形)の累積である。ヒモのどの部位を切り出しても,その部位の長さが同じであるかぎり,そこに見えてくる微小変形は同じものである。ここで今一度「ばねばかり」を思い出してほしい。伸びた分だけそれにかける力が大きくなる。そして,その「ばね」を固定している側には,かけている力と反対向きで同じ大きさの「反力」が存在する。この関係が,この局所的に切り出した部位すべてにおいて成立しているとイメージしても間違いはないようである。イメージできただろうか。短い「ばね」が鉛直方向に配列され,そのすべてが作用反作用の原理のもと,均等に伸びている様子がイメージできれば,その「小ばね」一つひとつにかかっているものが「内力」である。この内力を建築・土木系では「応力」と定義しているのである。目標は「応力度」の理解である。もう少しである。
「ばね」からヒモにイメージを戻そう。物理的な定義でのばねには断面はないが,ヒモにはリアルな断面がある。部位ごとに切り分けられた微小長さのヒモの両端には「内力」がかかっている。形全体が静かに釣り合っているときは,部位も同様に静かにその空間で釣り合っている。部分的に振動している状況はまだかなり先のことである。その微小ヒモの一つの断面に内力がかかり,それと同じ大きさで反対向きの内力がもう一つの断面に同時にかかっている。向きのこととなる内力が,微小ヒモ両断面にかかり均衡しているのである。さて,このヒモがちぎれる時をさらにイメージしてみよう。伸ばして伸ばしていくと,その断面のどこからからほころびが生まれてくるであろう。いきなり同時に全体がぶちと切れることはないであろう。断面それぞれを構成する分子レベルの材料配列にも同様にその力はかかるのである。しかし実のところはこのレベルまで来ると厳密な定義はほぼ不可能である。形あるものを最後まで厳密扱おうとすることの限界がそこにある。
工学はこの点便利である。実測もしくは経験則的に現象を定義し,ものづくりに生かすことができる。この工学的な,それもかなり初等的な応力の定義として,「応力」=内力/断面積を紹介したい。単位としては内力はニュートン[N]であり,断面積は平方メートル[m2]である。つまり,応力の単位は[N/m2]であり,これをパスカル[Pa]と書くこともどこかで聞いたことがあるであろう。この[Pa]は,上図の応力解析結果の凡例の一部に106を示すメガ[M]と一緒に書き込まれていることに気付いてほしい。ここで長々と説明を試みている応力と,すでに柴モクレンの花びらで解析した応力とは次元的には同一のものである。もちろんここでは引張変形に関連する応力の説明しかしていないので,花びらが受けている複雑な変形にそのまま持っていけるものでもないが,おおざっぱさを許してもらえるものとするなら,花びらの表(上側)には引張が主にかかり,裏側には圧縮がかかる傾向にあるのは,花びらに限らず,このように一端だけが固定されて水平方向に展開する形,構造においては一般的な応力の分布傾向である。花びらに関してはさらに,ねじれてしまうことも無視できないので,引張,圧縮に加えて長方形を平行四辺形に変形させるような「せん断」に関連する応力も忘れてはならない。純粋に材料力学的にこの手の話をしようとすると,大体このあたりから雲行きが怪しくなる。
図7,図8の凡例横に示されているVon Mises(フォンミーゼス)はミーゼス応力とか等価応力とが呼ばれる応力の定義の一つであり,引張,圧縮,せん断のすべての変形による応力を,その応力の正負ではなく総合的な大きさがその構造への影響の度合いをシンプルに示すとする考え方の下で,算出されている。つまり,引張にしても圧縮にしてもねじれにしても,特定に部位に生じる応力の強さを明解に示す指標であり,多くのCAE(Computer Aided Engineering)のパッケージおいてデフォルトの応力表示となっている。
この応力に続いて,避けることのできない「モーメント」が待っているのだが,少なくとも花びらの凄さ,健気さを知るにはこれぐらいでまずは良いかなと考えている。
蜘蛛の巣の形 The shape of a spider's web

雨上がりの蜘蛛の巣の形は,何かが違う。捕獲用のネットに微妙な曲面が生まれている。おそらく,蜘蛛の糸には,その主である蜘蛛の体重と比較すると,人間では決してまねができないほどの強い張力が掛かっていることだろう。晴れた日の風がない時の蜘蛛の巣のこの面の張りは緊張感を持った平面を構成する傾向にある。ところが,このように順序良く数えきれないほどの雨粒がその糸にぶら下がってくると,なんとも言えない有機的で自然とも言える形が見えてくる。
There seems to be a small difference in the shape of a spider's web after rain to the normal shape that is optimized for capturing insects. Perhaps the spider's thread is under so much tension when compared to the weight of its spider that humans can't hope to imitate it. The tension on the cobweb tends to form a tense plane if there is no wind on a sunny day. However, when countless numbers of raindrops hang down from the thread in good order, the web shows us an organic and natural curved surface.
It's a wonderful shape. It's a real, living web structure. A spider is in the centre and we can feel a firm tension no matter what part we look at. The intersection of radials and spirals embodies the geometrical and organic form of the overall structure. The tension is applied to all parts of the web, and it suggests that the tensile stresses are distributed in the cross-sections of all spider threads.1. 典型的な蜘蛛の巣の形 Typical spider's web shape
見事な形である。中央には蜘蛛が控え,生きたネット構造である。どの部位を見ても緩みなく張りを持っている。短線と短線との交叉によって全体構造としては,幾何学的かつ有機的な形を具現化している。すべての部位に張力がかかり,すべての蜘蛛の糸の断面には引張応力が分布していることになる。
The shape is magnificent. It is a living net structure with a spider in the center. Every part of the structure is taut and secure. The overall structure embodies a geometric and organic form, due to the intersection of short lines and short lines . All parts of the web are under tension, which means that tensile stresses are distributed across the cross-sections of all the spider threads.

図1 蜘蛛の巣を構成する同心円状の周方向の糸と放射状の径方向の糸
蜘蛛が首尾よく,すべての部位において均等な張りを持たせながら彼の仕事場を作ることができたとするなら,このネットはより平面的で,アジアングッズとして目にするドリームキャッチャーのような形になるであろう。ところが,全体的に張りを維持しつつ緩やかに曲面を構成している。特にこの日の降雨によって,規則正しく糸にそって雨粒が配置され,さらにその曲面は際立っているように見える。
If the spider were able to successfully create his work area with equal tension in all parts, this net would be flatter, much like the Asian product known as a dreamcatcher. However, it is composed of a gently curved surface while maintaining overall tension. In particular, raindrops are arranged regularly along the threads, and the natural surface seems to appear to be more distinguished by the rain in daylight.

図2 雨粒が分布するたわむ蜘蛛の巣
この曲面はいったい何なのか。蜘蛛の巣は3次元曲面を構成しているので,そう簡単に分析することはできない。このようになかなか難しい形に立ち向かうときは,まずは2次元に落とし込んで分析することを試みる。
What is the nature of this surface? Since the spider's web consists of a 3-dimensional surface, it is not so easy to analyze it. When we are confronted with such a difficult shape, often a good way of analyzing it – perhaps surprisingly – is to simplify it to two dimensions.
2. 蜘蛛の巣の形の単純化 Simplifying the shape of a spider's web
蜘蛛の巣そのものの構造学的特徴を,リアルな形のままに解析することも今となっては可能になってきている。しかしながら,電卓同様に,結果がすぐ出る道具を,その原理もわからないままに使っていると,かけ算そのものもわからくなってしまう。そこで何が起きているのか,その形の成り立ちの本質的な要素は何なのかなどを明解に知るためには,“うまい”単純化は必須なものとなってくる。
ここでは,中央から外周に向けて放射状に展開する糸の一本(図1中の黄色の線)に注目し,その糸が受ける外的条件いいかえると境界条件を,その糸モデルとともに再現することを目的とする。
It has become possible nowadays to analyze the structural characteristics of a spider's web as it is in its realistic form. However, as with a calculator, if we use a tool that produces immediate results without understanding its principles, we will not be able to understand the calculation itself. In order to know clearly what is happening and what are the essential elements of the formation of the form, "good" simplification is essential.
In this topic, we focus on a particular thread (yellow line in Fig. 1) that develops radially from the center to the periphery, and try to reproduce the external conditions or the boundary conditions to which this thread is subjected as well as the thread’s model.

図1 モデル化される径方向の糸
図1中の黄色の糸を主と考えるとき,この同心円状の蜘蛛の巣の周方向(赤線)に配置され,そして黄色の糸と交差する周方向の糸の存在は,交差点における集中荷重で表現できると考える。
If we consider the yellow thread in Figure 1 as the main thread, certain circumferential threads (red lines) which intersect the yellow thread can be represented as a concentrated load at the intersection.
周方向の糸をダイレクトに扱うのではなく,その構造力学的な存在価値を等価な集中荷重(図2中で黄線にそって周期的にバネを介して配置された質量)に置き換えるとする考え方である。さらに,図1の中で光る雨粒の列は,ほとんどの質量を持たないとみなすことができる糸にそって密に点在しているので,その効果も入れるために,糸を現す黄色の短柱にも適度な質量を与えている。図2は,初期状態では水平に配置され,全く同じ状況で離散的に集中質量が負荷された7本の短柱が,重力の影響を考慮した物理シミュレーションにより,振動しながらも,ある一定の釣り合い状態に収束した様子を示している。蜘蛛の巣がなんらかの力を受け,振動し,そして落ち着いたときに見せる形をモデル化したものとでも理解してもらえると問題ないかと考える。
The idea is not to treat the circumferential thread directly, but to replace the effect of intersecting the circumferential threads and the yellow line to its structural dynamic value with an equivalent concentrated load (the mass periodically arranged through the spring along the yellow line in Figures 1 and 2). In addition, since the rows of shining raindrops in Figure 1 are densely scattered along the thread (which can be regarded as having little mass), the short yellow columns representing the thread in Figure 2 are also given a moderate mass in order to include this effect. Figure 2 shows how the seven short pillars, initially placed horizontally and loaded with discrete concentrated masses under exactly the same conditions, converged to a certain state of balance while oscillating in a physical simulation that takes into account the effect of gravity. The upper waveform in Fig. 2 is the result of physical simulation from the time when the effect of gravity starts to be applied until the curve naturally stabilizes. It can be understood as a model of the shape of a spider's web when it is subjected to some kind of force, vibrates, and then settles down.

図2 2Dにモデル化された径方向に糸
このシミュレーション結果より,径方向の糸の中央寄りの端と外周側の端には,大きさが同じで向きが180度異なるFTが存在することを可視化している。この径方向の糸が,重力環境下のもので,水平方向には外力なく釣り合っていることがわかる。
From the results of the simulation, it is visualized that there is a set of FTs of the same size but with different orientations (180) at the central and peripheral ends of the radial thread (Fig.2). It is suggested that these radial threads are in a gravitational environment and are in balance, with no horizontal external forces.
図3 短柱ごとの力関係
さらに,この力関係を短柱ごとに見ていくとのように,どの部位の短柱であってもその両端にかかる内力はFTであり,必ず短柱ごとに水平方向の力の釣り合いを成立させるために同じ大きさで180度異なる方向にあることが確認できる。図1および図2において観察できる曲線の成り立ちは,重力と糸方向の張力のみとの力のバランスに支配されていると気づくことができる。重力は水平方向の成分は持たないため,各部位における水平方向の力FTは,すべての部位において向きが異なり同じ大きさのFTとのセットで存在しなければこの左右のバランスを成立させることはできない。
Furthermore, if a dynamic force relationship were estimated for each short column (yellow rod), the internal force at both ends of the column should be the FT, which is always of the same magnitude and in a different direction by 180toach other in order to establish the horizontal internal force balance for each short column. It also suggests that the formation of the curves observed in Figs. 1 and 2 is governed by the balance of forces between gravity and the tension in the thread direction which matches the direction of the short column locally. As gravity does not have a horizontal force component, the horizontal force FT at each short column must be present in a set with two FTs of the same magnitude and inverse direction in order for this left-right balance to be established.
また,糸上に点在する雨粒による鉛直方向の力に釣り合いうものは,糸が伸びる方向に発生する張力(引張力)の鉛直方向の力の成分であることは理解できる。つまり,この形を支配するものは,糸が伸びる方向にしか存在できない力(張力/内力・引張力)の鉛直方向の成分と重力の釣り合い,および,相対する水平方向の力の成分同志の釣り合いによって形成されていると理解することができるわけである。
ここでもし,周方向の糸との交叉点で径方向の糸が受ける断続的な力の影響が,径方向に一様に分布している雨粒による負荷荷重の影響により,その断続な力の流入が無視できるとするなら,糸全体に均等な重力による力(物体力)がかかり,テンション構造(張力場構造)特有の有名な曲線に近づくことに気が付くであろう。その有名な曲線は懸垂曲線(懸垂線/カテナリーカーブ)と呼ばれるものであり,シンプルな力と形の関係を容易に具現化してくれるものとしては大切な曲線形状である。
If the influence of the intermittent force which the radial thread is subjected to at the point of intersection with the circumferential thread is negligible, due to the influence of the load imposed by the raindrops uniformly distributed in the radial direction, then a uniform gravitational force (object force) will be applied to the whole thread, and the curve will finally approach the famous curve characteristic of tension structures. This famous curve is called a suspension curve (or catenary curve), and it is an important curve shape as it easily realizes a real and sophisticated relationship between force and form.
懸垂曲線を体験することはとっても容易である。材質は問わない。ただ,くしゃくしゃとしてもそれに抵抗することなく引張力を受けること以外に全く興味をしめさないものである必要がある。少しでも曲げられることに抵抗を示す素材であると,この曲線の繊細な形と力のバランスは乱されることになる。It is very easy to experience a suspension curve. The material composing the curve does not matter. It is only necessary that the material should not resist being bent if it is crumpled, and it is not at all interested in anything other than being subjected to a tensile force. If the material resists being bent in any way, the delicate shape of the curve and the balance of forces will be disturbed.
図4 引張力と重力との釣り合いの形,懸垂曲線
蜘蛛の巣を単純化していくと,膜やロープで構成される大型の建造物にもみられる懸垂曲線の形が,そこに存在することを確認することができる。懸垂曲線にしても蜘蛛の巣にしても,全体に張力,引張応力が分布し連続する見事に張りのある形であると言える。そしてこの形は意外と身近なところで目にすることができる。
The simplification of the spider's web confirms the existence of a suspension curve, which is also found in large buildings made of membranes suspended from cables. Both the suspension curve and the spider's web have a wonderfully taut form, with tension and tensile stress distributed throughout. And this form can be seen in many places around us.
図5 電線も懸垂曲線
3. もう一つの蜘蛛の巣の形 Another form of spider's web
前述したように蜘蛛の巣を構成する要素は糸であり,糸は引張応力のみを受け止めることができる素材なので,その糸によって構成されるすべての部位に連続して張力がかかる構造でなければ,その美しい形は成立しない。そしてその構造的特徴ゆえに,雨粒などによる負荷荷重を受けることで,張力を受けることを主とする構造では,いたって自然な形状である懸垂曲線がそこに現れることを理解した。
As mentioned above, the element that makes up a spider's web is thread, and since thread is a material that can only take tensile stress, the beautiful shape of a spider's web can only be achieved in a structure where tension is applied continuously to all the parts that are composed of the thread. And because of this structural characteristic, it has been understood that a suspension curve, which is a very natural shape, appears in the structure that mainly receives tension by being loaded with raindrops continuously distributed on the threads.
ところが,ステレオタイプともいえる同心円群と放射状の糸による蜘蛛の巣ネットのイメージを揺るがす形態に遭遇することができた。However, I have met a web that did not conform to the stereotypical image of a spider’s web with concentric circles and radial threads.
図6 箱状の蜘蛛の巣
この形の中には同心円も放射状のものも見当たらない。この巣の主(オレンジ色に光っている)も,わかりやすく中央付近にいるのではなく,なんとも自由な位置にて待機している。
There are no concentric circles or radial shapes in this shape. The owner of the nest (glowing orange) was not in the centre of the nest, but was waiting for something in a very free position.
箱状の巣の中をランダムに張り巡らされた糸の存在は朝日の反射で確認できるものの,そこに規則性を見出すことはできない。ただ言えることは,この箱の底面の曲面を除いては,すべての部位において比較的同じ密度で糸が様々な方向に配置されているようにうかがえる。ランダムな配置にもかかわらず,全体に均等さがうかがえ構造体としての軽やかささえ感じ取ることができる。そして驚くべきは,この蜘蛛の巣もどの部位を見ても緩みやたるみがなく,リズミカルなほど張りを保っている。つまり,すべての部位においてその糸は適切な引張応力を受け,重力や風力,枝から葉を通して伝わる振動による外力とうまくバランスを取っていると理解できる。その中でも底の曲面の緊張感は見事であり,この蜘蛛の建築家としての才能をうらやむほどである。Although the presence of threads randomly stretched through the box-like web can be confirmed by the reflection of the morning sun, no regularity can be found there. The only thing that can be said is that the threads seem to be arranged in various directions with relatively the same density in all areas, except for the curved surface at the bottom of the box. In spite of the random arrangement, there is an evenness to the whole structure, and one can even feel the lightness of the structure. What is surprising is that this spider's web is not loose or sagging in any part, but remains rhythmically taut. In other words, in every part of the web, the threads are subjected to appropriate tensile stresses and are well balanced with external forces such as gravity, wind, and vibrations transmitted from branches through leaves. The tension of the curved surface at the bottom is so especially impressive that I would envy this spider's talent if I were an architect.
図7 底部の形状
近づいて見ると底部の小構造はより細やかであり,この箱状巣の他の側面や内部には見ることのできない連続した構造である。さらには下の枝から上に伸びる数本の糸によって,その底面は緊張感をもって引き下げられており,優雅な三次元曲面を構成している。
ここでも,考察を明解にするために,この形の単純化を行う。
Closer inspection reveals a finer substructure at the bottom, a continuous structure that cannot be seen on any other side or interior of this box web. Furthermore, the bottom of the web is pulled down by tension provided by several threads extending upward from the branches below, forming a graceful three-dimensional curved surface.
Again, for the sake of clarity, I will simplify this form.
4. 箱状蜘蛛の巣底部の形の単純化
この底部にさらに近づいてみると,どこかで見たような曲線が見えてくる。どうも懸垂曲線を上下反転させたような形が見えてくる。そこで,この曲面の稜線を手掛かりに2Dモデル化を図る。
If you look closely at the bottom part of this structure, a familiar curve should be apparent to you. It looks like an upside-down version of a suspension curve. So another 2D model using the ridge line of this curve as a clue is to be defined.
図 底部に見られる逆懸垂曲線
この稜線を基準の糸と見立て,その稜線から前後に展開する底部メッシュシートの張力の影響は均等に分布するバネに置き換えることを考えた。必ずしも厳密なモデル化ではないが,形があることと力が分布し伝達していることは,特にこのような自然の形においては等価であるといっても間違いでないことが多い。
This ridge line is considered to be the reference thread, and the effect of the tension in the bottom mesh-like sheet that develops behind and in front of the ridge is replaced by an evenly distributed spring in the figure. This is not necessarily an exact model, but it is often the case that the existence of the shape and the distribution and transmission of the forces are equivalent, especially in natural shapes such as this one.
稜線だけを糸として残し,他はその稜線の糸に働きかける張力としてその存在を置き換えているのである。
Only the ridge is left as a thread, and the rest replaces the small springs and the weights as a tension acting on the thread of the ridge.

図 2Dモデル化された箱状蜘蛛の巣底部の稜線
The ridge of the bottom of a boxy spider web modelled in 2D
下枝からの牽引を受ける前の状態を「初期状態」とし,牽引力をかけてから構造全体の振動が治まるまでのシミュレーションを実施した。この結果,実際の稜線と同様な曲線を得ることができた。この2Dモデルにおける上部に配列されたバネ列により牽引される形は初期状態にも戻ろうとする復元力をこのバネ列から受けることになり,それが一般的な懸垂曲線を支配する重力同様に機能すると考えると,この上に凸の曲線も間違いなく懸垂曲線と同質のものであることが分かる。
この結果は,実は当然のことである。引張にしか耐えることのできない構造要素で構成される構造体は,その構造要素の軸方向を主軸とする引張力と構造全体にかかる外力との釣り合い関係においてのみ成立するわけなので,その形の基本的な造形原理は同一のものとなっても不思議なことではないだろう。
The "initial state" is defined as the state before the traction from the lower branch (initial state), and the simulation is carried out from the time at which the traction force is applied until the vibration of the whole structure subsides (after the vibration has subsided), in which the traction force is replaced with the two weights.
As a result, a curve similar to the actual ridge line is obtained. If we consider that the form of the traction provided by the upper row of springs in the 2D model is subjected to a restoring force from this row, which also tries to return to the initial state, and that this force acts in the same way as the gravitational force governing the general suspension curve, it seems that the upward convex curve is definitely of the same quality as the suspension curve.
フジヤマの形 Shape of Fujiyama
富士山の形の特徴の一つは,その斜面である。この山を題材とする浮世絵では,この斜面はもっと強調されており,実は富士山より富士山らしい。そのらしさ,もしくは形として魅力はどこからきているのだろうか。そこに何かの力学的な意味があるのだろうか。
ここでは,たまたま撮影できた富士山から,その形の特徴を抜き出し,フジヤマとしてモデル化することでその形に成り立ちについて考察する。
実際の形をそのまま扱うことは,無数の変数を扱うことと同じなので,富士山をそそり立つ円錐台に置き換え,フジヤマとの名称を与えた。
One of the characteristics of the shape of Mt. Fuji is its slope. In Ukiyo-e, which uses this mountain as a subject, this slope is more emphasized, and it's more like Fuji than the real Fuji. It raises important questions as to where the attractiveness of the shape comes from and whether there is a mechanical meaning, from the viewpoint of styling.
Here, we will examine the origin of the shape by extracting the characteristics of that shape from a chance photograph of Mt. Fuji and modeling it as FUJIYAMA.
To analyze the actual form directly would entail handling a myriad of variables, so we have replaced Fuji with a truncated cone shape composed of many small discs stacked in layers to simplify the shape and have given this truncated version the name FUJIYAMA.
1. 富士山のトレースと層分割 Tracing and Stratification of Mt. Fuji
富士山が成層火山であることも踏まえて,形の基本構成を「積層」と捉え,単純化することを試みた。イラストレータを利用して,稜線のトレースと複数の層を分割した。Mt. Fuji is a stratovolcano, so I attempted to simplify the basic composition of the shape by "layering". Using Adobe Illustrator, I traced the ridges and divided the mountain into layers.
図1 稜線のトレースと層分割 Ridge tracing and layer segmentation
図1の層分割に従って,この富士山を図2のような円状の断面を持つ微小円錐台の積層によるフジヤマとしてモデル化した。山頂中央を原点として,鉛直方向下向きを正とする座標xを定義する。図中のAはx=x点での円錐台の断面積を示している。微小円錐台は高さΔxを持ち,図中に示してあるように,微小円錐台の上面の断面積がAであることに対して下面の断面積をA+ΔAと定義していることを示している。To produce the layer division as shown in Fig. 1, Mt. Fuji was modeled as a laminated Fujiyama of micro cones with a circular cross section as shown in Fig. 2. The center of the summit is the origin, and the coordinate x is defined as positive downward in the vertical direction. A in the figure shows the cross-sectional area of the cone at the x=x point. The micro cone has a height Δx, and the figure shows that the cross-sectional area of the upper surface of the micro cone is A, while the cross-sectional area of the lower surface is defined as A+ΔA.
図2 微小円錐台への分解とフジヤマの定義 Fujiyama composition by stacking micro cones
The cross section found when the shape of Mt. Fuji is viewed as a cone and the cone is broken down into smaller cones as shown in the figure.
フジヤマも重力下にあるので,この微小円錐台は,上面と下面からの圧力つまり圧縮応力とこの微小円錐台自身の重さ,自重を受けることになり,この3つの力のつり合いよって,この形が安定して成立することになる。Since Fujiyama is also under gravity, the micro-cone is subjected to pressure from the upper and lower surfaces, i.e., compressive stress, as well as the weight of the micro-cone itself, i.e. its own weight, and the balance of these three forces ensures that this shape is stable.
2. フジヤマの層間に掛かる圧縮応力 Compressive Stress between the layers of Fujiyama
高層ビルや煙突,タワーにおいても,当然なことであるが,下層ほど強い“力”が掛かり,構造的に辛いことを,誰しも直感的に理解できるであろう。この“辛さ”はどこから来るのだろうか。その辛さは構造体内部に分布し伝搬する内部の力つまり内力によるものであり,フジヤマはじめ様々な鉛直方向上向きに伸びる構造体においては,その主たる内力は,大地震や大台風でも来ない限り,重力による自重つまり物体力によって引き起こされる。そして,単純化してみると,その内力は鉛直方向を主軸として分布し,その軸に直交する各層の断面に圧縮力をかけることになる。その圧縮力は,下層の断面ほど大きくなる。
Insofar as such structures as skyscrapers, chimneys or towers can be pictured as structures consisting of many thin layers in which each layer has a mass, everyone intuitively understands that, the lower the layer of such a structure, the more “force” is applied to it and the more structurally painful it is.
Where does this "pain" come from? In Fujiyama and other vertical structures, the main internal force is caused by the weight of the structure due to gravity, unless there is a big earthquake or a big typhoon.
In a simplified way, the internal forces are distributed with the vertical direction as the main axis, and compressive forces are applied to the cross-section of each layer orthogonal to that axis. The compressive force increases with the cross-section of the lower layer.
さて,構造が壊れるとはどういう状況であろうか。構造を構成するものは材料であり,その材料を構成するものは分子構造である。構造が壊れる前に,それを構成する材料の局所的なとこらから不具合が発生し,全体への崩壊につながる。
Now, what is the situation when a structure is destroyed? The structure is made up of materials, which in turn are made up of molecular structures. Before the structure breaks down, there are local failures in the materials that make up the structure, leading to a collapse of the whole.
この局所的な崩壊と密接につながってくる一つの工学的な定義が応力(度)である。応力も実験的な定義からより現実的な局所の挙動を考慮した数理的な定義もあるが,ここではもっともシンプルな考え方を紹介したい。
One engineering definition which is closely linked to this local collapse is stress (degree). There are experimental definitions of stress, as well as mathematical definitions which take into account more realistic local behaviour, but here I would like to introduce the simplest idea.
それは,いたってシンプルで,どこかでだまされているような感じもしてしまうかもしれないが,すべての複雑な現象を単純にみて,
It is so simple that it may seem to possess insufficient precision, but it is the simplest way of looking at all complex phenomena.
応力[ N/m2] = 内力 [N] / 断面積 [m2]
Stress [N/m2] = Internal force [N] / Cross-sectional area [m2].
と定義するだけである。応力の単位[ N/m2] は[Pa]とも記され,パスカルと読む。聞き覚えがある音であろう。圧力を表現するような音である。圧力と応力の単位は同じなので,やや混乱するかもしれないが,この単純化された形では,鉛直方向に圧縮力を与える単位面積あたりの圧力だと思っていても力学的な感覚としてはそれほど大きな問題は起きないように思われる。
This stress is simply defined as the unit of stress [N/m2] which is also written as [Pa]. When it is expressed in terms of Pascals it may sound more familiar and sound like a representation of pressure.
The units of pressure and stress are the same, which may be somewhat confusing to our understanding, but in this simplified form of Fujiyama it might not cause too much trouble in the mechanical sense to think of it as the pressure per unit area of vertical compressive force.
図3 フジヤマの層間に掛かる圧縮応力
Compressive stresses between the layers in Fujiyama
一般的に,構造の主軸の方向にかかる応力は一般的にσ(シグマ)と表記される。気になってしまう人のために参考までに示しておくと,その主軸に対して斜め45度で定義される応力にせん断応力というものがあり,それはτ(タウ)と記される。σもτも実は出所は同じなので,内力を受けているものをどのように見るかでそれぞれの応力の出番が変わってくる。ここでは鉛直方向に分布する圧縮応力σだけを見ておけば十分である。
In general, stresses in the direction of the main axis of a structure are denoted by σ (sigma). In case you are interested in this kind of engineering region, there is another stress defined at 45 degrees diagonally to the principal axis called shear stress, which is denoted by τ (tau). σ and τ actually come from the same source, so how you look at the internal stresses will affect how each stress appears or governs the engineering state. Here, I think it is sufficient to look only at the compressive stress σ, which is distributed vertically.
さて,フジヤマであるが,その構造は,おそらく,すべての部位において同じ素材と同じ局所構造の繰り返しで全体構造つまり形が構成されていると理解しても,それほど間違ってはいないであろう。そのことは,どの部分においても同様な力学的特性があるとみなしてもいいとの考えである。
It would not be too far wrong to understand that the structure of Fujiyama is probably composed of the same material and the same local structure repeated in every part of the whole structure or form in the vertical direction. That is to say, we may assume that the same mechanical properties are present in every part of the layers and the interfaces.
このフジヤマの形が,その自重に耐えられる限界の形であると仮定してみよう。耐えられるぎりぎりに尺度としては,前述の圧縮応力σが最適である。
Let us suppose that the shape of Fujiyama is the limit of what it can bear under its own weight. The best measure of the limit of endurance is the aforementioned compressive stress σ.
なぜなら構造体の崩壊は,このケースでは,その構造を構成する材料の局所的な破綻から始まるからである。この限界時の応力を「強度」と定義することができる。一般的にはこの「強度」が幅広い意味において使用される傾向にあるが,ここでは,単位面積当たりにおいて受け止めることができる内力の大きさを,つまり受け止められる限界の応力を強度と定義する。したがって,図3中のσは,強度ぎりぎりの圧縮応力が,その層間すべてにおいて発生しているとイメージすれば良いことになる。
This is the reason why the collapse of a structure begins, in this case, with the local failure of the materials of which it is composed. The stress at this limit beyond which a collapse will begin can be defined as the "strength" of a structure. In general, "strength" tends to be used in a broad sense, but here we define strength as the stress at the limit of the internal force that can be accepted per unit area. Therefore, σ in Fig. 3 can be imagined as the compressive stress at the limit of strength occurring in all the layers.
直感的に,もしくは経験的に考えても,全体を構成する部分に配分されるタスクは均等であることが一番都合がいいように思われる。部分である材料がすべて均等にσを受け止めればいいわけである。
Intuitively, or even empirically, it seems most convenient that the tasks allocated to the parts of the whole should be equal. It is only necessary that all the parts, the materials, should receive equal force of σ.
フジヤマでは鉛直方向のみの応力への意識で良いので,この応力は図に示すように,山頂からふもとまで,すべての層間において,青色の短い矢印群で示した同じ大きさの圧縮応力が均等に分布している状況をイメージしてもらえればいい。
In Fujiyama, we need to be aware of stresses in only the vertical direction, and these stresses can be imagined as a situation where compressive stresses of the same magnitude, indicated by the short blue arrows, are evenly distributed between all the layers, from around the summit to the foot, as shown in the figure.
図3では山頂から8番目の層についてのみで表現しているが,この応力の分布は,すべての層間において存在すると理解してほしい。ただ,一層抜き出してみると,このように見えてくるのだが,元に戻すと,層間の応力は,まさに作用反作用の関係にあり,一見打ち消しあって消滅しているように見えてしまうところが難しいところである。しかしながら,それであっても奴らはそこに潜在し,崩壊のチャンスを狙っている。
In Fig. 3, the stresses are represented only for the eighth layer from the summit, but it should be understood that similar the stress distribution exists between all the layers. However, if we take out one layer, we can see it like this, but if we put it back in the structure, the stresses between the layers are exactly action-reaction relationship, and it is difficult to see that they seem to cancel each other and disappear. But even so, they are still there, latent, waiting for the chance to collapse it.
3. 層における力のつり合いとフジヤマの形 The balance of forces in the layers and the shape of Fujiyama
フジヤマを構成する層の形は,高さが微小な円錐台である。ここでは微積的な考え方で微小としている。したがって,一層に相当する微小円錐台の体積は,層ごとに,その上面の面積×鉛直方向下向きの座標つまりxの微小部分つまりΔxに,円錐台の上面の断面積Aを掛けることで算出している。円錐台の体積はそれでは間違っている!との思いもあるかとは思うが,ここでは“微小”ということで,微積の慣例に従い,その差は無視できるものとさせていただく。したがって,層ごとに微小円錐台の体積 × ρ(密度)× g(重力加速度)が自重(物体力)として,フジヤマの山頂からふもとに向けて加算されていくことになる。
The shape of the layers that make up Fujiyama is a truncated micro cone. I use the term micro here in the calculus sense. Therefore, the volume of the micro cone corresponding to a single layer is calculated for each layer by multiplying a small part of its downward vertical coordinate x, i.e. Δx, by the cross-sectional area of the upper surface of the cone, A. That's not the right volume for the small truncated cone but in this case the difference from the right volume of the cone generally seems to be negligible, following the conventions of calculus, because it is "tiny". Therefore, for each layer, ‘the volume of the micro cone’ בρ (density)’בg (gravitational acceleration)’ is serially added from the top to the bottom of Fujiyama as a part of the whole weight (body force).
この自重に対して力のつり合いを取るのが,σである。
図4 微小円錐台の力のつり合い
図4中の下向きの太めの黒矢印が,それぞれの層群の自重を表している。ここでは,微小円錐台における力のつり合い式は,下向きの力と上向きの力が等しいと考えれば,以下のようになる。
これが,まさにフジヤマの形を数理的に表現するものであり,モチーフとなった富士山の形との類似性を否定できるものではなく,その形の成り立ちの一部を示すものと理解している。
蛇足であるが,そして余談であるが,式の展開部分の見た目が変わっているのは,数式を書くのにMoodleのHTMLでは面倒であったので,LaTexを使用してみた。興味がある人はLaTexを体験してほしい。


コメント
コメントを投稿